DesignSeries00053.pngSpring Calculator

The spring calculator can determine spring rates and unit stresses of round wire helical coil compression springs with known parameters. It can also be used to design a spring knowing the working values. This example is based on the following compression spring with closed and ground ends of music wire.

springrate_example.png 

To calculate spring rate and unit stress:

  1. Determine the required spring rate based on the deflection at a load divided by the difference in the working length and the free length. For this example, the desired spring rate equals 28.8 lb/in (36 lb/1.25 in = 28.8 lb/in).

  2. Select the Spring Calculator command from the appropriate menu:

    3. ●    Architect workspace: AEC > Machine Design > Spring Calculator 

    ●    Landmark workspace: Landmark > Machine Design > Spring Calculator 

    ●    Spotlight workspace: Spotlight > Machine Design > Spring Calculator 

    The Spring Calculator dialog box opens.

    spring_method1.png 

  3. As shown in the above dialog box, select 1 - Outside Dia., Wire Dia., Solid Height from the Method list. After entering the known values, calculate a spring rate close to the desired value by trying several standard wire diameter values. Adjust the material in the Material list to fit the wire diameter used. Here, a wire diameter of .090” gives a spring rate of 8.94 lb/in.

  4. In the Method list, select 2 - Mean Dia., Wire Dia., No. of Active Coils.

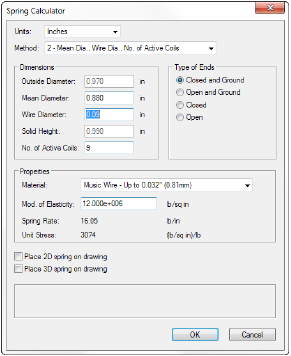
    5. spring_method2.png 

  5. As shown in this dialog box, vary the wire diameter and number of active coils to get a spring rate close to the required spring rate. A wire diameter of .095” and 11 active coils gives a spring rate of 16.3 lb/in, but the solid height is 1.24”, which is too high. A wire diameter of .090” and 9 active coils, however, gives a spring rate of 16.1 lb/in, and a solid height of .990”, which is within acceptable limits.

  6. Finally, check the stresses applied to the spring to verify that they are within acceptable limits. With a unit stress of 3074 (lb/sq in)/lb, multiply by 36 to obtain 110,663 lb/sq in. With a solid height of .990”, the stress will be:

    7. (2.500-0.900)in x 16.1 lb/in x 3074 (lb/sq in)/lb = 79,200 lb/sq in

  7. This value is below the safe working stress of 111,000 lb/sq in for this material and wire size.

 

vectorworks.net