
La curva Spline Beta racional no uniforme (NURBS, por sus siglas en inglés) es una fórmula matemática que representa la geometría de curvas, círculos, arcos y superficies en el espacio 3D. Las superficies y curvas de forma libre pueden crearse y editarse con un alto nivel de flexibilidad y precisión.
Una curva NURBS generalmente consiste en un valor de grado y puntos de control de peso o vértices. La curva pasa entre los puntos de los vértices; el grado determina cuántos puntos afectan la curva. La dirección indica el punto inicial y el punto final de la curva mientras se dibujaba, lo que puede afectar el resultado de determinadas operaciones.

El aumento del peso relativo de uno de los vértices significa que el vértice tiene más de una influencia en la curva y "desplazará" la curva hacia el vértice.

La herramienta Transformar se puede usar para mover un vértice o varios vértices, cambiando la forma de la curva (vea Transformar curvas NURBS).

El aumento del grado de una curva NURBS aumenta proporcionalmente la cantidad de vértices, lo que permite más flexibilidad en el dibujo de la curva y también más complejidad debido a los numerosos pesos que afectan la curva.

Los mismos principios que aplican a la curva NURBS aplican a la superficie. Una superficie NURBS es una cuadrícula o malla de puntos de control ponderados en las direcciones U y V.
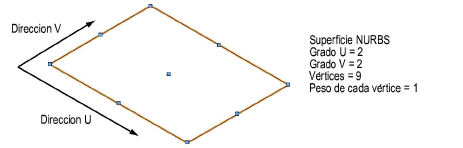
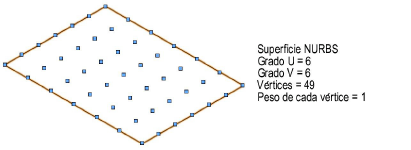
El aumento del grado de una superficie NURBS en la dirección U o V aumenta el número de vértices, agregando flexibilidad al igual que complejidad.
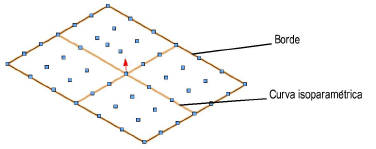
Una superficie NURBS también tiene una dirección, o normal, que afecta el resultado de determinadas operaciones, como la creación de la superficie empalmada. Las curvas isoparamétricas indican la dirección U y V, y las curvas de bordes se dibujan a lo largo de los bordes ayudando a visualizar la superficie NURBS.
Cada vértice de la superficie puede tener un vértice que "desplaza" la superficie hacia los vértices de peso.
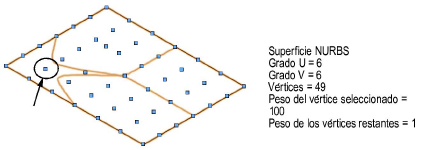
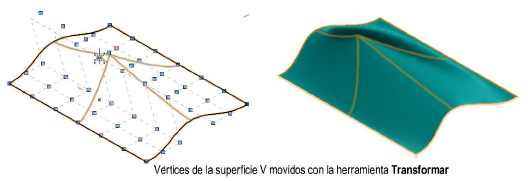
La herramienta Transformar puede mover un vértice simple o un a fila de vértices, deformando la superficie (vea Transformar superficies NURBS).
Las curvas y superficies NURBS se pueden definir mediante puntos de control o puntos de interpolación. La curva o superficie pasa entre puntos o a través de puntos de interpolación.

Las curvas y superficies interpoladas pueden ser más sencillas de modificar. Vea Crear curvas NURBS y Superficies NURBS interpoladas.
Se pueden crear formas complejas y de forma libre con las curvas NURBS y las superficies NURBS. Luego las formas se pueden combinar, cortar, agregar, recortar, extender, analizar o de otra forma modificar según se describe en estas secciones.
Haga clic aquí para ver un video consejo acerca de este tema (requiere acceso al Internet).
~~~~~~~~~~~~~~~~~~~~~~~~~
